Legend on the Origin of Chess
A charming legend surrounds the invention of chess, attributed to the wise Indian scholar Sissa ben Dahir over 2000 years ago.
India was ruled by the young and unjust King Shahram. The learned Sissa ben Dahir devised the game of chess to enlighten the king. He showed that even a humble pawn could decide the game: "Behold, Your Majesty, even a small pawn can determine the outcome! And we, the pawns, the common people, must be taken into account."
Modest Reward for the Chess Invention?
The king learned from the game and asked the scholar what reward he desired for his invention. The scholar only requested a humble gift: that the king place on the first chessboard square one grain of wheat, on the second two grains, on the third four grains, on the fourth eight, and so on, doubling for each subsequent square.
While the king appreciated the scholar's modesty, the reward seemed too small. Insisting on his request, the king sent wheat collectors throughout vast India. Shockingly, the report returned: there wasn't enough wheat in all of India to satisfy the scholar's wish!
Mathematical Calculation
Initially angered, the king calmed down after the scholars explained that the grains needed would be:
264 - 1 = 18,446,744,073,709,551,615.
An astronomical number exceeding 18 quintillion! How did we arrive at this number? Simply by doubling 1, 2, 4, 8, 16, 32, etc. (although the numbers grow rapidly later), as shown in the chessboard image below, and summing the grains on all squares.
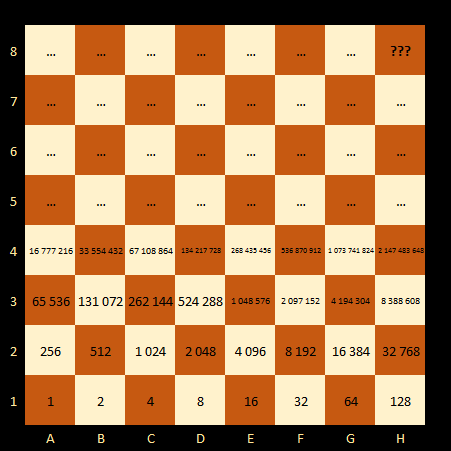
Figure 1: Chessboard with Wheat Grains on Each Square
We can also consider the sum of previous squares to equal the square of the number minus one. For example, take square H1, where 27 = 128. The sum of previous squares is 1 + 2 + 4 + 8 + 16 + 32 + 64 = 127, i.e., 27 - 1 = 127. On square A1, it's 20, and on the last square H8, it's 263. Imagining an imaginary 65th square, the sum of grains on all 64 chessboard squares is the aforementioned 264 - 1.
| Square | Number of Grains | Square | Number of Grains |
|---|---|---|---|
| 1 | 1 | 33 | 4,294,967,296 |
| 2 | 2 | 34 | 8,589,934,592 |
| 3 | 4 | 35 | 17,179,869,184 |
| 4 | 8 | 36 | 34,359,738,368 |
| 5 | 16 | 37 | 68,719,476,736 |
| 6 | 32 | 38 | 137,438,953,472 |
| 7 | 64 | 39 | 274,877,906,944 |
| 8 | 128 | 40 | 549,755,813,888 |
| 9 | 256 | 41 | 1,099,511,627,776 |
| 10 | 512 | 42 | 2,199,023,255,552 |
| 11 | 1,024 | 43 | 4,398,046,511,104 |
| 12 | 2,048 | 44 | 8,796,093,022,208 |
| 13 | 4,096 | 45 | 17,592,186,044,416 |
| 14 | 8,192 | 46 | 35,184,372,088,832 |
| 15 | 16,384 | 47 | 70,368,744,177,664 |
| 16 | 32,768 | 48 | 140,737,488,355,328 |
| 17 | 65,536 | 49 | 281,474,976,710,656 |
| 18 | 131,072 | 50 | 562,949,953,421,312 |
| 19 | 262,144 | 51 | 1,125,899,906,842,624 |
| 20 | 524,288 | 52 | 2,251,799,813,685,248 |
| 21 | 1,048,576 | 53 | 4,503,599,627,370,496 |
| 22 | 2,097,152 | 54 | 9,007,199,254,740,992 |
| 23 | 4,194,304 | 55 | 18,014,398,509,481,984 |
| 24 | 8,388,608 | 56 | 36,028,797,018,963,968 |
| 25 | 16,777,216 | 57 | 72,057,594,037,927,936 |
| 26 | 33,554,432 | 58 | 144,115,188,075,855,872 |
| 27 | 67,108,864 | 59 | 288,230,376,151,711,744 |
| 28 | 134,217,728 | 60 | 576,460,752,303,423,488 |
| 29 | 268,435,456 | 61 | 1,152,921,504,606,846,976 |
| 30 | 536,870,912 | 62 | 2,305,843,009,213,693,952 |
| 31 | 1,073,741,824 | 63 | 4,611,686,018,427,387,904 |
| 32 | 2,147,483,648 | 64 | 9,223,372,036,854,775,808 |
| The total number of grains on all squares: 18,446,744,073,709,551,615. | |||
Where to Get So Much Wheat?
Looking at the chessboard, the grain count seems to grow slowly at first, with only 128 grains at the end of the first row. However, moving up another row, the number of grains dramatically increases, reaching over 9 quintillion grains on the 64th square. This is a number that wouldn't be shameful for any numerical lottery in terms of combinations.
Mathematicians calculated that for King Shahram to fulfill Sissa ben Dahir's wish, it would require so much wheat that it would cover the entire surface of the Earth in 10 years, including seas and oceans (which constitute about 70% of the Earth's surface)!
Doubling the number of grains on each square follows a geometric (not just arithmetic) progression and resembles the Martingale system, famous especially in Roulette, where a player consistently bets on the same color until it hits, doubling bets in case of loss. The chessboard above illustrates how bets can escalate in the event of a longer losing streak. We've also tested the Martingale system.
Finally, it's worth noting that this charming legend about the origin of chess is not based on truth. Chess originated around 600 AD in India or Persia and its rules were gradually modified to their present form.
