Mega Millions
Mega Millions is a number lottery that is played in the United States of America. The historically biggest jackpot worldwide (as of 17 April 2014) was hit right in this game. The jackpot amounting to $656 million was split among three players.
How to Play Mega Millions
The players of Mega Millions pick 5 white balls out of 75 and 1 golden ball out of 15. They can use their own lucky numbers or automated easy pick. There are nine prizes in total, similarly as in another US lottery Powerball.
The top prize is the jackpot, the other eight prizes are fixed. The minimum jackpot is $15 million, but it increases by at least $5 million per drawing (the state of rules as of 17 April 2014). The jackpot is won by one or more player(s) who match all 6 drawn numbers, that is 5 + 1. As for the other prizes they depend on how many white balls (out of 5) are hit by a player and whether or not the golden number is caught. The ticket costs $1.
Odds of Winning (and Losing)
The odds of winning any of the nine prizes, and additional information, can be found in the Table 1 below. If you succeed to match 5 out of 5 drawn numbers (out of the total of 75 numbers or white balls) and 1 golden ball (out of 15 golden balls in total), then the jackpot is yours.
If you only match 5 + 0, then you win the 2nd prize. The fixed prizes (no. 2 to 9) are taken from the Mega Millions operator web site (see the source under the Table 1). The jackpot as the top prize is floating, therefore—for the needs of our calculations (mainly of the player's expected average outcome)—we use its average value of about $103 million (source: lottostrategie.com, quoted 2014-04-17).
How many combinations may occur when drawing 5 balls out of 75 and 1 ball out of 15? We can use the Excel formula =COMBIN(75,5)*COMBIN(15,1) or shortly =COMBIN(75,5)*15 and we arrive at the value of 258,890,850 possible combinations. Only one combination of six numbers (5 + 1) is winning the jackpot, therefore the odds of winning the jackpot in Mega Millions is:
1 in 258,890,850, which equals to the probability1 ÷ 258 890 850 = 0.00000000386263168435655.
Table 1: The Prizes and Odds of Winning and Losing in Mega Millions
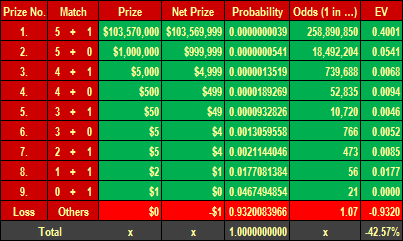
Source: the $ prizes taken from the Mega Millions web site (quoted 2014-04-17), own table design and calculations
The probabilities of winning the other prizes in Mega Millions are also shown in the Table 1. If we add up all winning probabilities, we get the probability of winning at least something; that is approximately 0.068 or 1 in 14.7 (1 ÷ 0.068). On the other hand the probability of leaving empty-handed is the remainder to one (or 100%). Thus the probability of not winning anything in Mega Millions is 0.932 (93.2%) or 1:1.07.
→ The relation between odds and probability.
Let us add that you can also pay $1 more for so called Megaplier that multiplies the fixed prizes.
Expected Average Outcome of Long-term Betting
We know the probabilities of winning as well as the prizes that can be won. We also know the probability of losing $1 per a ticket. The column Net Prize considers the initial $1 bet.
If we multiply the net prizes and the loss of the $1 bet by the probabilities of winning and losing, we will arrive at the (partial) so called expected values (EV). By adding up the partial EVs we get the expected value -0.4257 or -42.57%. It shows the expected average outcome of the long-term betting of the Mega Millions lottery.
It means that, in the long run, the player loses in average about 43 cents on each dollar invested in the game. That is the margin of the operator of Mega Millions. It always holds true that player’s loss is house’s gain and vice versa. So if the expected value of the player is negative, then the expected value of the lottery company (or casino or house in general) is positive.
What If You Win – Payout Options
Winners can choose two ways of being paid out: cash option or annuity option. The first case is a one-time payment, but subject to federal 35% tax. The annuity option consists of one immediate payment followed by 29 annual payments, while each payment is 5% bigger than the previous one. The payments used to be equal. According to the company the players demanded this way in order to cover increasing costs of living.
→ Lottery Games
→ EuroJackpot
→ EuroMillions
→ Keno
→ Mega Millions
→ 10-spot Keno
→ Powerball
→ Scratch Cards
Source: Mega Millions (the original Czech article).
