Powerball
Powerball is a U.S. number lottery. On Wednesday 28 November 2012 there was a record jackpot of $587.5 million that was shared by two winners. The odds of winning the jackpot are 1 in 175 million. Let us have a close look at the game, its probabilities and expected return in the long run.
How to Play Powerball
In the lottery Powerball there are drawn five (5) white balls out of fifty-nine (59) and one (1) red ball out of thirty-five (35) also known as the Powerball. There are nine prizes based on how many regular white balls are matched by a player and also whether the powerball (1 of 35) is hit or not.
The jackpot is the Powerball's top prize. The minimum jackpot is $40 million (as of 30 November 2012). To win the jackpot means that the player must match all 5 numbers (out of 59) and the powerball (1 of 35). The other prizes are fixed, for example the 2nd prize is $1,000,000. If the player catches at least the powerball, he or she will not leave empty-handed. The ticket costs $2. Drawings take place on Wednesday and Saturday.
Odds of Winning (and Losing)
Table 1 shows all important characteristics of the lottery game Powerball including the probabilities (or the odds) of winning any of the nine Powerball prizes. The column "Match" says how many numbers (0 to 5) out of 5 drawn numbers (and 59 numbers in total) is necessary to match to get the prize. The next column "Powerball" is important as well, whereas "yes" indicates whether the powerball needs to be hit or not.
As we know, except for the first prize (the top prize or the Powerball jackpot) the lower prizes are fixed. The minimum guaranteed jackpot is $40 million. For calculations we use the average jackpot of $255 million, the figure that is published on the Powerball website. The prizes have no influence on their probability of winning, but as we will see below, the varying jackpot changes the expected value, which represents player's expected return in the long run as well as the Powerball operator's edge (or margin).
The columns "Netto Prize" and "...as a multiple" are auxiliary for the calculation of the expected value (EV). The netto win can be calculated easily by deducting $2 (initial bet) from the prize. And if we divide this figure by $2 we get the netto win as a multiple. That is useful as then we can get the player's expected outcome of each dollar wagered in the game. If we deduct this from 100% we arrive at the player's expected long-term return.
Table 1: The Prizes & the Odds of Winning in the Powerball Lottery (USA)
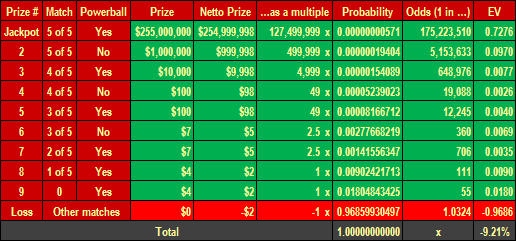
Source: Prizes & matches – the Powerball official website (quoted as of 2012-11-30), own calculations and design
The probability of winning the jackpot in Powerball is very low. How do we find it out? As always we are interested in how many unique combinations can be created in this lottery game. We can simply use the Excel function: =COMBIN(59,5)*COMBIN(35,1). In common words we would like to know how many groups of five (with 59 total numbers) and a single number (with 35 powerballs) can be created. The result is 175,223,510 unique combinations. And since only one combination is winning, the probability and the odds of winning the Powerball jackpot is the following:
1 ÷ 175,223,510 = 0.00000000570699673805187 or 1 in 175,223,510.
Table 1 shows the probabilities of winning the lower prizes as well. If we add up all winning probabilities we get the probability of winning at least something, precisely 0.03140069503 or 3.14% or 1 in 31.85. The total of probabilities must equal 1 (or 100%). Therefore the probability of leaving empty-handed is about 0.9686 = 96.86% = 1 in 1.0324.
→ The odds of winning the jackpot in Mega Millions.
Player's Expected Return in the Long Run
Now let us calculate the margin of the Powerball operator and the player's expected return of the long-term betting. As usually we use the expected value (EV) that adds up all individual prizes (and a loss of bet) weighted by their probabilities. Thus the expected value considers both prizes and their probabilities. It is a mean value or a long-term average.
As we mentioned before, only the jackpot (the 1st prize) is varying. For calculations we use the average jackpot $255 million (published by the gaming company). The product of the "Netto Prize" and "...as a multiple" times the "Probability" gives the first partial result for the calculation of the expected value (0.7276). We go on row by row and finally add it all up and arrive at the wanted expected value (house edge / margin) -0.0921 or -9.21%. The lower is the margin, the better for the player. Such a low margin means that the player's long term return is 100% – 9.21% = 90.79%.
This looks very optimistic for the player. It depends a lot on the amount of jackpot. Therefore we tried to use the minimum guaranteed jackpot $40 million and the expected value has dropped to -70.56%, and thus the player's long-term return is about 30% only. We also tried to raise the jackpot somewhere in between, namely to $120 million. Then the expected value is -47.73% and the return is 52.27%. These calculations suggest that each invested dollar would return only 30 or 52 cents.
We can summarize the expected values of varying levels of the jackpot:
- Jackpot $40,000,000: EV = -70.56%,
- Jackpot $120,000,000: EV = -47.73%,
- Jackpot $255,000,000: EV = -9.21%.
In all cases the expected value is calculated from the player's point of view. The essence of gambling and lottery games is that it is negative for the player. The same but positive value applies for casinos as it holds true that the player's loss equals the casino's gain.
Power Play
Power Play is a possibility to spice up the game, however the player stands in front of a dilemma. The ticket costs an additional $1. Power Play raises the fixed prizes – they are approximately a double of the normal prizes – but it does not apply to the jackpot. Is it worth it?
It depends how we look at it. The odds of winning are the same as in the normal game and you can win more, however for more money invested. So, from the short-term point of view and being extremely lucky it may pay off, but in the long run it is necessary to look what the expected value says. As we can see at the Table 2, the player's expected value is -70.95%. It means that you are going to lose about 70 cents of each dollar wagered in Powerball Power Play. That is much higher than in the "normal" game.
Table 2: Powerball Power Play – Expected Return
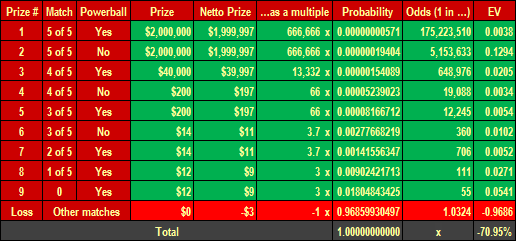
Source: Prizes & matches – see the Powerball official website (quoted as of 2012-11-30), own calculations and design
Prizes Payout
The winners of Powerball must face one more but pleasant dilemma. They may cash the prize at once, but it is subject to the federal income tax of 35%, or they may get the whole prize tax-free in 30 installments during the next 29 years.
→ Lottery Games
→ EuroJackpot
→ EuroMillions
→ Keno
→ Mega Millions
→ 10-spot Keno
→ Powerball
→ Scratch Cards
Other resources: Powerball (original Czech article).
